Pythagorean Theorem Proof is not so New

MSN reports:

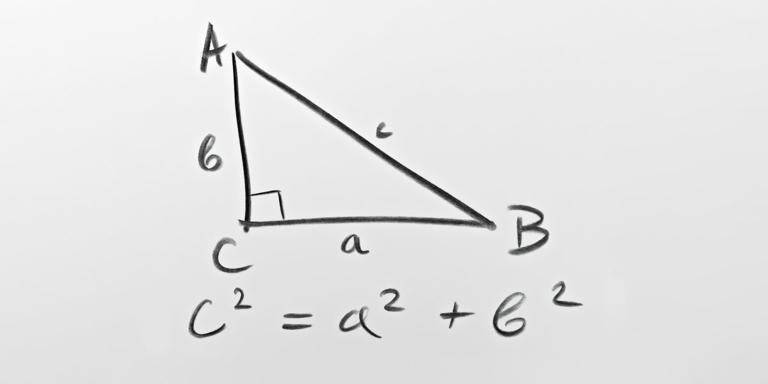
The Pythagorean Theorem — discovered by the Greek mathematician Pythagoras in the 6th century BCE — is a cornerstone of mathematics. Simply stated as a² + b² = c², the theorem posits that the sum of the two shortest sides of a right triangle (a² and b²) is equal to that triangle’s longest side (c²). For centuries, this idea has been proven by some of history’s greatest minds, such as Albert Einstein, U.S. President James Garfield (of all people), and even Pythagoras himself.

In fact, there have been hundreds of proofs of the Pythagoras’ groundbreaking theorem, but almost none of them — if not none at all — have independently proved it using trigonometry. That’s because the fundamentals of the theorem are what the entire field of trigonometry is built on, and so, the thinking goes that to use trigonometry to prove the theorem is to employ what’s called “circular reasoning.” It’s essentially using the Pythagorean Theorem to prove the Pythagorean Theorem.

Some mathematicians argue that using trigonometry to independently prove the theorem is actually impossible, including Elisha Loomis, whose book on the topic (originally published almost a century ago) states that “there are no trigonometric proofs because all the fundamental formulae of trigonometry are themselves based upon the truth of the Pythagorean theorem.”

No, this is ridiculous. There are lots of trignonometric proofs.

Here is one.

sin α = a / c
cos α = b / c
Area = ab/2 = c²(.5 sin α cos α)

This means that the area of any right triangle is given by the square of the hypotenuse, multipled by a trigonometric function of the angles.

Now drop a perpendicular from C to c, dividing the triangle into two smaller similar triangles. The area of the big triangle equals the sum of the areas of the two smaller ones. The big one has hypotenuse c, while the smaller ones have hypotenuses a and b. Thus a² + b² = c², after dividing by that common trigonometric factor. The factor is the same for all three triangles, because the angles are the same.

This uses trigonometry, but does not use the identity (sin²α + cos²α = 1).

The supposed new proof is much more complicated, and uses limits.